SPC汽车零部件质量管理解决方案

【导读】
摘要：介绍统计过程控制(SPC)的原理及其在汽车零部件质量管理中的应用。以某沉孔深度为控制对象。利用SPC统计学方法对其加工尺寸进行分析，并根据分析情况采取相应措施，从而达到
摘要：介绍统计过程控制(SPC)的原理及其在汽车零部件质量管理中的应用。以某沉孔深度为控制对象。利用SPC统计学方法对其加工尺寸进行分析，并根据分析情况采取相应措施，从而达到过程失控预警、过程不断改进、过程能力不断提高的目的，继而保证产品质量的稳定和可靠。
 
引言
    汽车零部件的加工通常是由多个生产过程来完成的，零件的加工质量和各个过程的工序能力息息相关。目前，大多数汽车零部件生产企业通过产品检验并剔除不合格品来保证产品质量，这种事后检验的方法忽略了对制造过程的控制和改进，既浪费了材料和人力，也降低了产品质量信息的可靠性。如何保证产品的质量并使生产过程能力不断提高就变得很有意义。本文主要介绍了统计过程控制技术及其在汽车零部件生产过程控制中的应用。


1  SPC定义
    统计过程控制(SPC)主要是指应用消除异常，恢复过程的稳定，从而达到提高和控制质量的目的。统计分析技术对生产过程进行实时监控，科学地区分生产过程中产品质量的随机波动与异常波动，从而对生产过程的异常趋势提出预警，以便生产管理人员及时采取措施，消除异常，恢复过程的稳定，从而达到提高和控制质量的目的。
 
    SPC理论源于20世纪20年代，以美国质量大师休哈特(W．A．Shewhart)博士发明控制图为标志，自创立以来即在工业和服务等行业得到推广应用。二战中美国将其制定为战时质量管理标准：50年代，SPC引入日本，被广泛应用于汽车工业；80年代则开始在美国汽车、钢铁工业中大规模推行。IS09000族质量体系和美国三大汽车工业集团的QS9000认证也将SPC作为一项重要内容。


2 SPC控制原理和常规控制图
2．1 SPC控制原理
    SPC的理论基础是中心极限定理和3σ原则中在生产过程中，当众多彼此相互独立的偶然因素共同对生产对象产生影响时，由于彼此的相互作用、相互抵消，而最终使产品的质量特性呈正态分布。根据正态分布的重要结论可知，在正常生产情况下，质量特性在区间μ±σ的产品为68．25％；在区间μ±2σ的产品为95．45％；在区间μ±3σ的产品为99．73％(其中μ为质量特性值的平均值，σ为其标准偏差)。 这说明凡是在μ±3σ范围内的质量差异都是正常的，不可避免的，是偶然性因素作用的结果，如果质量差异超过了这个界限，则是系统因素造成的。

    在生产过程中，产品加工尺寸的波动是不可避免的，它是由人、设备、材料、工艺方法、测量方法以及环境等基本因素的波动影响所致。按照产品质量特性值波动的情况，可将影响因素分为偶然因素和系统因素。其中偶然因素对生产过程一直起作用，这类因素对质量波动的影响不大，一般情况不会超出工序规格范围，所以在经济上并不值得消除，在技术上也是难以测量和避免的。系统因素只在一定时间内对生产过程起作用，但将造成较大的质量波动，所以这类因素是必须消除的，同时在技术上也是易于识别、测量且可以消除和避免的。图1给出了制造过程中的变异源，便于质量管理人员查找原因，改进过程，从而提高过程的稳定性和工序能力。
 
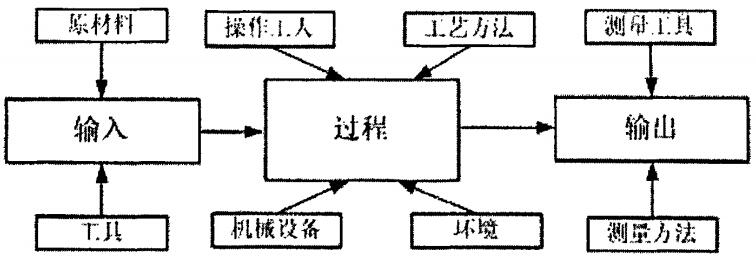
图1 制造过程中的变异源


2．2常规控制图
    控制图是对过程质量加以测定、记录从而进行评估和监察过程是否处于控制状态的一种用统计方法设计的图，如图2所示。图上有中心线(CL)、上控制界限(UCL)、下控制界限(LCL)，并有按时间顺序抽取的样本统计量。若控制图中的描点落在UCL与LCL之间的排列不随机，则表明过程异常，需查明原因、采取措施、设法消除。
 
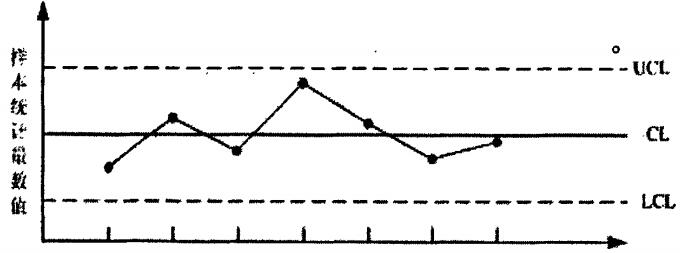
图2 控制图示例
 
    控制图对过程的监控是通过抽查来进行的，既然是抽查，依据控制台的控制界限所作的判断也可能发生错误。这种可能的错误有两类：第一类错误是将正常的过程判为异常，即虚发警报。在正常情况下，打点出界限的可能性为0．27％，根据小概率事件原理，认为其不可能发生，但如果生产过程正常而点子偶然出界，根据点出界就判异，就犯了第一类错误；第二类错误是将异常判为正常，即漏发警报。
 
    过程已经异常，但仍会有部分产品的质量特性值在上下控制界限之内，如果恰巧抽取到这样的产品，描点就会都在界内，从而犯了第二类错误。扩大控制限会增大犯第二类错误的概率，而减小控制限会增大犯第一类错误的概率。当采取3σ原则确定控制限幄度时，两类错误的概率总和最小，这也是统计过程控制技术遵循3σ原则的原因所在。

    根据控制图所控制数据类型的不同，控制图可分为计量值控制图和计数值控制图。计量值控制图一般适用于计量值为控制对象的场合，包括均值一极差控制图(χ-R控制图)、均值一标准差控制图(χ-S控制图)、中位数一极差控制图(χ—R控制图)以及单值一移动极差控制图(χ-Rs控制图)等。计数值控制图又可分为记件值控制图和计点值控制图，记件值控制图包括不合格品率控制图(P控制图)和不合格品数控制图(Pn控制图)，计点值控制图包括单位不合格数控制图(u控制图)和不合格数控制图(c控制图)。根据控制图的用途和应用场合不同，控制图可分为分析用控制图和控制用控制图。分析 用控制图用在生产过程控制之初，主要任务是判断过程稳定与否和是否存在异常因素。控制用控制图是在过程稳定且满足技术要求的情况下，由分析用控制图转化而来的，主要任务是对过程进行日常监控，以便及时报警。


2．3 SPC的实施流程
    统计过程控制技术的实施过程为一个闭环系统。即通过确定关键质量控制点，分析其关键质量特性，确定数据采集方案和控制图类型，通过工序分析和工序能力计算，查找偶然因素和系统因素，并将追查信息及时反馈，以便于缩短产品延误时间，不断提高生产过程能力。具体实施步骤如图3所示：
 
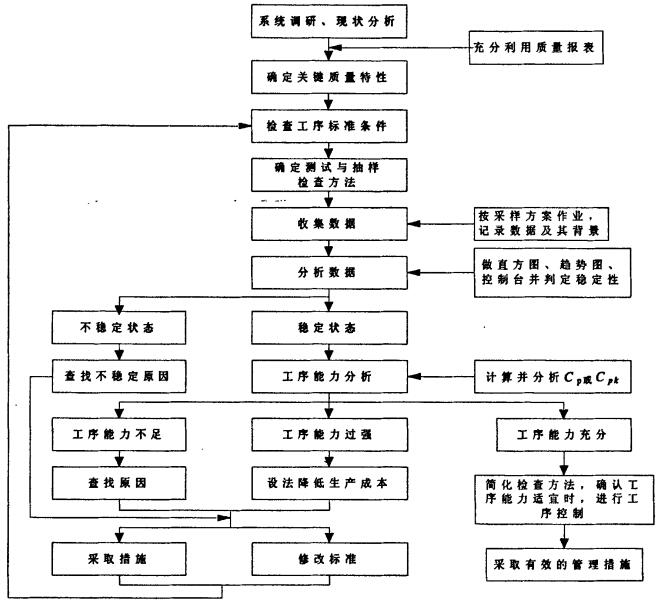
图3 统计过程控制实施流程


3汽车零部件生产过程控制
    下面以某后轴承盖沉孔深度为例，介绍统计过程控制在汽车零部件生产过程中的应用。沉孔深度要求为9．4950-0．015 mm。
    (1)质量数据收集方法
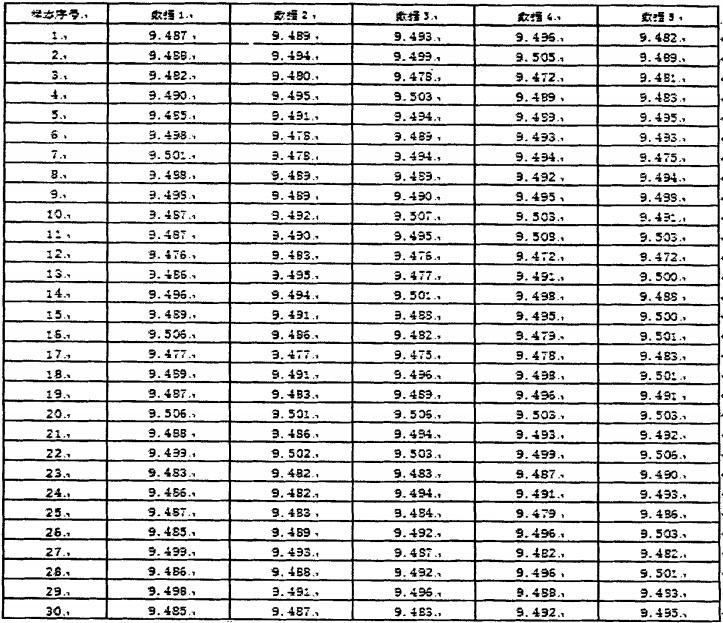
    〓 抽样方案：后轴承盖沉孔深度质量控制点是对沉孔深度尺寸进行质量控制。后轴承盖沉孔深度作为影响后轴承盖质量的主要质量特性，加工过程较复杂，而且尺寸要求严格，测量较困难，每天的产量为200-300件，所以根据后轴承盖的生产批量需要对该工序实施较长时间的抽样，同时为了保证控制图能有效地区分变差的特殊原因，以便于发现影响工序能力的所有可能因素。决定抽样方案为：每加工25个后轴承盖沉孔随机抽取一组作为抽检样本，每个样本由连续抽检的5个后轴承盖沉孔深度尺寸数据组成，即样本容量n=5；

    〓 样本个数：为更好的检验工序的稳定性，抽取30组样本；

    〓 SPC分析与控制方案：由于质量特性为计量型数据，采用均值一极差控制图进行分析与控制。

    (2)数据收集
    根据抽样方案抽取样本，并测量质量特性值，所得30组数据如表1所示。
    表1后轴承盖沉孔深度检测记录
 
 
    (3)数据分析
    根据控制图的判断准则，极差图处于稳态。再分析均值图，从图中可以看出，第3、12、17、20、22五个样本超出控制界限，控制图过程不稳定，存在异常原因，调查发现：加工沉孔的道具损坏，导致加工尺寸不能严格的保障，需要替换新道具。

    剔除异常的样本点后，重新绘制控制图，发现过程处于稳态，可知影响产品质量的异常因素已经排除。将抽样数据导入到E-SPC中，自动生成控制图，如图4所示。
 
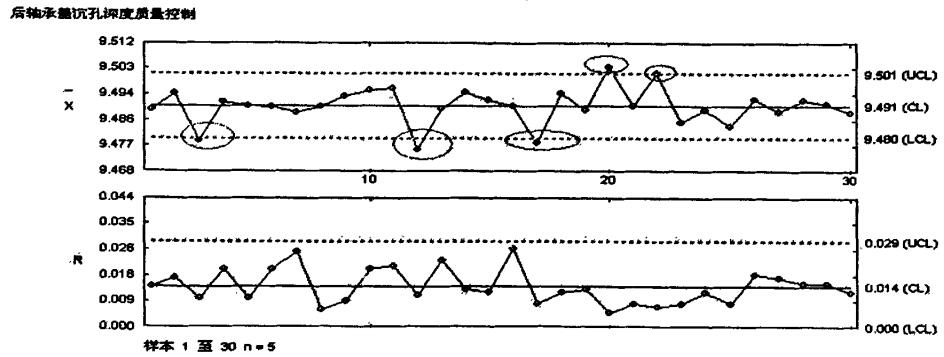
图4 后轴承盖沉孔深度控制图(初始图

    更换刀具后10天，重新采集数据，绘制控制图如图5所示，过程已经处于稳态。可以对后轴承盖沉孔深度工序进行工序能力评价。如图6所示，Cp=1．17，Cpk=1.11，根据过程能力指数评价标准可知，过程能力尚可，技术管理能力较勉强，应进一步提高。
 
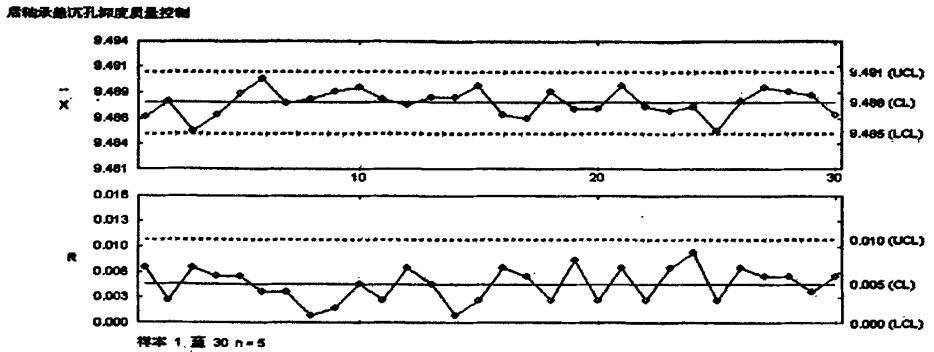
图5 后轴承盖沉孔深度控制图(改进后)
 
 
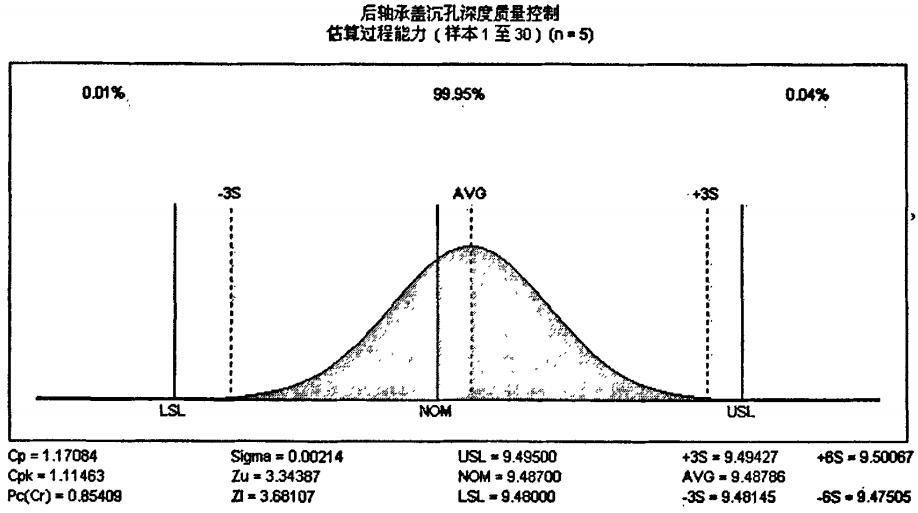
图6 后轴承盖沉孔深度工序能力图

 
4结束语
    本文介绍了SPC技术的基本原理，并通过实例说明了统计过程控制技术在汽车零部件生产过程中的应用。SPC技术的引用极大的提高了生产过程的稳定性和工序过程能力。在产品质量和可靠性日益重要的今天，应在企业中大力推广普及统计过程控制技术。 


  • 2019-07-22 16:21
  • 我要分享：
声明：文章"SPC汽车零部件质量管理解决方案"为上海御云信息科技有限公司原创文章，转载请注明出处,谢谢合作！您所在位置：FMEA系统 > 质量管理系统资讯 > SPC资讯 >

联系清泰代表

热门文章
热门标签